本文是多体量子理论课程计算部分的一道习题的个人解答，题目大概是写一个求解 $\mathrm{HeH^{+}}$ 两原子体系的 Restricted Closed-shell Hartree-Fock 方程的 SCF 程序。个人所用参考资料如下：
- 基组数据
- A. Szabo 和 N.S. Ostlund 写的 Modern Quantum Chemistry
- 理论参考了 https://zhuanlan.zhihu.com/p/677955631
- 程序有参考 https://qiita.com/hatori_hoku/items/867fa793488ebe1d2beb#fn14，这告诉我了非常重要的一点，要对本征值排序
- https://zhuanlan.zhihu.com/p/72016333 这里面的课程报告很有用，但有点问题
理论
此题在原子单位制下进行，要求对 $\mathrm{He H^{+}}$ 两原子体系的 Restricted Closed-shell Hartree-Fock 方程进行自洽场求解，设定原子距离为 $R = 1.4632 \ \mathrm{a.u.}$，体系包含两个电子，采用 STO-3G minimal basis set，查阅资料可得基函数形式上有 \(\phi(\vb*{r}) = \sum_{p = 1}^{4} C_p \chi(\alpha_p, \vb*{r})\)，其中 \(\chi (\alpha, \vb*{r}) = (2 \alpha / \pi)^{3 / 4} \ee^{- \alpha r^2}\)，对于氢原子基函数 $\phi_{1}$ 和氦原子基函数 $\phi_{2}$ 有 \(\begin{equation} \begin{aligned} \phi_{1} (r) & = C_1 \chi(3.425250914, r) + C_2 \chi(0.6239137298, r) + C_3 \chi(0.168855404, r), \\ \phi_{2} (r) & = C_1 \chi(6.362421394, r) + C_2 \chi(1.158922999, r) + C_3 \chi(0.3136497915, r), \\ & C_1 = 0.1543289673, \ C_2 = 0.5353281423, \ C_3 = 0.4446345422 \end{aligned} \end{equation}\) 注意到它们都是实函数，取复共轭等于自身。下面计算重叠积分矩阵 $S$，基函数是归一化的，所以必有 $S_{11} = S_{22} = 1$，故只需计算非对角项，而又有对称性 $S_{12} = S_{21}$，所以只需计算一个： \(\begin{equation} S_{12} = \int \dd{\vb*{r}} \phi_1 (\vb*{r} - \vb*{R}_1) \phi_2 (\vb*{r} - \vb*{R}_2) \end{equation}\) 这个三重积分直接计算是有点挑战的，但是注意到我们选择的基函数是由 Gaussian 函数线性组合的，利用 Modern Quantum Chemistry 一书的附录 A 可以直接得到 \(\begin{equation} \int \dd{\vb*{r}} \chi(\alpha, \vb*{r} - \vb*{R}_1) \chi(\beta, \vb*{r} - \vb*{R}_2) = \qty[\frac{4 \alpha \beta}{(\alpha + \beta)^2}]^{\frac{3}{4}} \ee^{- \frac{\alpha \beta}{\alpha + \beta} \abs{\vb*{R}_1 - \vb*{R}_2}^2} \end{equation}\) 则简单代入计算即可得到重叠积分矩阵 \(\begin{equation} S = \mqty[1 & 0.53681935 \\ 0.53681935 & 1] \end{equation}\)
对于动能积分矩阵 \(\begin{equation} T_{ij} = \int \dd{\vb*{r}} \phi_i(\vb*{r} - \vb*{R}_i) \qty(- \frac{1}{2} \laplacian) \phi_j (\vb*{r} - \vb*{R}_j) \end{equation}\) 同样有类似的化简式 \(\begin{equation} \int \dd{\vb*{r}} \chi(\alpha, \vb*{r} - \vb*{R}_i) \qty(- \frac{1}{2} \laplacian) \chi(\beta, \vb*{r} - \vb*{R}_j) = \frac{2^{\frac{3}{2}} (\alpha \beta)^{\frac{7}{4}}}{(\alpha + \beta)^{\frac{5}{2}}} \qty[3 - \frac{2 \alpha \beta \abs{\vb*{R}_i - \vb*{R}_j}^2}{\alpha + \beta}] \ee^{- \frac{\alpha \beta}{\alpha + \beta} \abs{\vb*{R}_i - \vb*{R}_j}^2} \end{equation}\) 计算可得动能积分矩阵 \(\begin{equation} T = \mqty[0.76003188 & 0.19744319 \\ 0.19744319 & 1.41176317] \end{equation}\)
对于电子与核吸引能矩阵 \(\begin{equation} V^{ne}_{ij} = \int \dd{\vb*{r}} \phi_i(\vb*{r} - \vb*{R}_i) \qty(- \sum_{I} \frac{Z_I}{\vb*{r} - \vb*{R}_I}) \phi_j (\vb*{r} - \vb*{R}_j) \end{equation}\) 内部求和是原子核 $I$ 进行的，$Z_I$ 是相应的核电荷数，在本题情况下有两个原子核。利用 Fourier 变换，可以得到化简式 \(\begin{equation} \int \dd{\vb*{r}} \chi(\alpha, \vb*{r} - \vb*{R}_i) \qty(- \frac{Z_I}{\vb*{r} - \vb*{R}_I}) \chi(\beta, \vb*{r} - \vb*{R}_j) = - \qty[\frac{4 \alpha \beta}{(\alpha + \beta)^2}]^{\frac{3}{4}} \frac{Z_I \ee^{- \frac{\alpha \beta}{\alpha + \beta} \abs{\vb*{R}_i - \vb*{R}_j}^2}}{\abs{\vb*{R}_{ij} - \vb*{R}_I}} \erf(\abs{\vb*{R}_{ij} - \vb*{R}_I} \sqrt{\alpha + \beta}) \end{equation}\) 其中 Gauss 误差函数定义为 $\erf(z) = \frac{2}{\sqrt{\pi}} \int_0^{z} \dd{t} \exp(- t^2)$，\(\vb*{R}_{ij} = (\alpha \vb*{R}_i + \beta \vb*{R}_j) / (\alpha + \beta)\)，注意到 \(\vb*{R}_{ij} = \vb*{R}_I\) 是特殊情况，使用 L’Hôpital 法则可得 \(\begin{equation} \int \dd{\vb*{r}} \chi(\alpha, \vb*{r} - \vb*{R}_i) \qty(- \frac{Z_I}{\vb*{r} - \vb*{R}_I}) \chi(\beta, \vb*{r} - \vb*{R}_j) = - (4 \alpha \beta)^{\frac{3}{4}} \frac{2 Z_I}{(\alpha + \beta) \sqrt{\pi}} \ee^{- \frac{\alpha \beta}{\alpha + \beta} \abs{\vb*{R}_i - \vb*{R}_j}^2} \quad (\vb*{R}_{ij} = \vb*{R}_I) \end{equation}\) 最终代入计算可得电子与核吸引能矩阵 \(\begin{equation} V_{ne} = \mqty[-2.49185755 & -1.6292717 \\ -1.6292717 & -4.01004618] \end{equation}\)
最后考虑双电子积分矩阵 \(\begin{equation} V^{ee}_{ijkl} = \int \dd{\vb*{r}_1} \dd{\vb*{r}_2} \phi_i(\vb*{r}_1 - \vb*{R}_i) \phi_j(\vb*{r}_1 - \vb*{R}_j) \frac{1}{\abs{\vb*{r}_1 - \vb*{r}_2}} \phi_k(\vb*{r}_2 - \vb*{R}_k) \phi_l(\vb*{r}_2 - \vb*{R}_l) \end{equation}\) 和之前类似，能得到化简式 \(\begin{equation} \begin{aligned} & \int \dd{\vb*{r}_1} \dd{\vb*{r}_2} \chi(\alpha, \vb*{r}_1 - \vb*{R}_i) \chi(\beta, \vb*{r}_1 - \vb*{R}_j) \frac{1}{\abs{\vb*{r}_1 - \vb*{r}_2}} \chi(\gamma, \vb*{r}_2 - \vb*{R}_k) \chi(\delta, \vb*{r}_2 - \vb*{R}_l) = \\ & \frac{64}{\abs{\vb*{R}_{ij} - \vb*{R}_{kl}}} \frac{(\alpha \beta \gamma \delta)^{\frac{3}{4}}}{[4 (\alpha + \beta) (\gamma + \delta)]^{\frac{3}{2}}} \erf \qty(\abs{\vb*{R}_{ij} - \vb*{R}_{kl}} \sqrt{\frac{(\alpha + \beta) (\gamma + \delta)}{\alpha + \beta + \gamma + \delta}}) \ee^{- \frac{\alpha \beta}{\alpha + \beta} \abs{\vb*{R}_i - \vb*{R}_j}^2 - \frac{\gamma \delta}{\gamma + \delta} \abs{\vb*{R}_k - \vb*{R}_l}^2} \end{aligned} \end{equation}\) 其中如前定义有 \(\vb*{R}_{kl} = (\gamma \vb*{R}_k + \delta \vb*{R}_l) / (\gamma + \delta)\)，注意到 \(\vb*{R}_{ij} = \vb*{R}_{kl}\) 是特殊情况，使用 L’Hôpital 法则可得 \(\begin{equation} \begin{aligned} & \int \dd{\vb*{r}_1} \dd{\vb*{r}_2} \chi(\alpha, \vb*{r}_1 - \vb*{R}_i) \chi(\beta, \vb*{r}_1 - \vb*{R}_j) \frac{1}{\abs{\vb*{r}_1 - \vb*{r}_2}} \chi(\gamma, \vb*{r}_2 - \vb*{R}_k) \chi(\delta, \vb*{r}_2 - \vb*{R}_l) = \\ & 128 \frac{(\alpha \beta \gamma \delta)^{\frac{3}{4}}}{[4 (\alpha + \beta) (\gamma + \delta)]^{\frac{3}{2}}} \ee^{- \frac{\alpha \beta}{\alpha + \beta} \abs{\vb*{R}_i - \vb*{R}_j}^2 - \frac{\gamma \delta}{\gamma + \delta} \abs{\vb*{R}_k - \vb*{R}_l}^2} \sqrt{\frac{(\alpha + \beta) (\gamma + \delta)}{\pi (\alpha + \beta + \gamma + \delta)}} \quad (\vb*{R}_{ij} = \vb*{R}_{kl}) \end{aligned} \end{equation}\) 最终代入计算可得双电子积分矩阵 \(\begin{equation} \left\{ \begin{aligned} V^{ee}_{1111} & = 0.77460594 \\ V^{ee}_{1112} & = 0.36741016 = V^{ee}_{1121} = V^{ee}_{1211} = V^{ee}_{2111} \\ V^{ee}_{1122} & = 0.59080731 = V^{ee}_{2211} \\ V^{ee}_{1212} & = 0.22431934 = V^{ee}_{1221} = V^{ee}_{2112} = V^{ee}_{2121} \\ V^{ee}_{1222} & = 0.44396499 = V^{ee}_{2122} = V^{ee}_{2212} = V^{ee}_{2221} \\ V^{ee}_{2222} & = 1.05571294 \\ \end{aligned} \right. \end{equation}\)
到此，我们已经计算出了所有可以预先计算的矩阵元，方便了后续的迭代过程。Roothaan 矩阵方程可写作 \(\begin{equation} F C = S C \epsilon \label{math:1} \end{equation}\) 其中 $F$ 被称为 Fock 矩阵，是 Fock 算符 \(f(\vb*{r}) = h(\vb*{r}) + \sum_{b=1}^{N} [J_b(\vb*{r}) - K_b(\vb*{r})]\) 的矩阵表示，$J_b$ 与 $K_b$ 分别被称为 Coulomb 算符和交换算符，在本题中，我们考虑闭壳态，即两个电子占据相同的轨道但拥有不同的自旋，所以有 \(f(\vb*{r}) = h(\vb*{r}) + \sum_{a=1}^{N / 2} [2 J_a(\vb*{r}) - K_a(\vb*{r})]\)，写成矩阵有 \(\begin{equation} F_{ij} = H_{ij}^{\text{core}} + \sum_{a = 1}^{N / 2} 2 \obraket{ij}{aa} - \obraket{ia}{aj} \end{equation}\) 其中 $N$ 是电子数量，$H_{\text{core}} = T + V_{ne}$ 称为 core-Hamiltonian 矩阵，单电子积分只和单原子的基态波函数相关，故我们之前的计算得到的结果在迭代过程中它是不变的，但是双电子积分显然不一样，依赖于系数矩阵 $C$，电子波函数定义为 $\psi_i = \sum_{\mu=1}^{N} C_{\mu i} \phi_i$，则应该有 \(\begin{equation} F_{ij} = H_{ij}^{\text{core}} + \sum_{a = 1}^{N / 2} \sum_{k, l} C^{*}_{k a} C_{l a} [2 V^{ee}_{i j k l} - V^{ee}_{i l k j}] \label{math:2} \end{equation}\) 最后，电子密度与系数矩阵有关系 \(\begin{equation} \rho(\vb*{r}) = 2 \sum_{a}^{N / 2} \psi_a^{*}(\vb*{r}) \psi_a(\vb*{r}) = 2 \sum_{i, j} \sum_{a}^{N / 2} C^{*}_{i a} C_{j a} \phi^{*}_i(\vb*{r}) \phi_j(\vb*{r}) \end{equation}\) 电子总能为 \(\begin{equation} E_0 = \sum_{i, j} \sum_{a}^{N / 2} C^{*}_{j a} C_{i a} (H^{\text{core}}_{ij} + F_{ij}) \end{equation}\)
求解矩阵方程 \eqref{math:1} 是一个矩阵的本征值问题，对角化重叠矩阵 $U^{T} S U = s$，引入矩阵 $X = U s^{- 1/2}$，令 $C = X C’$ 且 $X^{T} F X = F’$，代入则有 $F’ C’ = C’ \epsilon$，这就转化成了本征值问题，故我们的 Hartree-Fock 自洽场算法步骤如下：
- 指定相应分子的数据，包括原子核坐标 \(\{\vb*{R}_A\}\)、核电荷数 ${Z_A}$、电子数量 $N$ 和一组基底 ${\phi_{i}}$
- 计算所有需要的单双电子积分矩阵 $S_{ij}$、\(H^{\text{core}}_{ij}\) 和 $V^{ee}_{ijkl}$
- 对角化重叠积分矩阵 $U^{T} S U = s$，获得变换矩阵 $X = U s^{- 1/2}$
- 给出初始猜测系数矩阵 $C$
- 根据式 \eqref{math:2} 计算 Fock 矩阵 $F$
- 计算变换后的 Fock 矩阵 $F’ = X^{T} F X$
- 对角化矩阵 $F’$ 获得 $C’$ 和 $\epsilon$
- 计算 $C = X C’$
- 判断当前系数矩阵是否收敛，不收敛则返回步骤 5
- 后处理，输出结果，绘制图像
程序与结果
我们使用 Python 语言进行了算法的实现，最后程序输出如下：
重叠积分矩阵：
[[1. 0.53681935]
[0.53681935 1. ]]
动能积分矩阵：
[[0.76003188 0.19744319]
[0.19744319 1.41176317]]
电子与核吸引能矩阵：
[[-2.49185755 -1.6292717 ]
[-1.6292717 -4.01004618]]
双电子积分矩阵：
[[[[0.77460594 0.36741016]
[0.36741016 0.59080731]]
[[0.36741016 0.22431934]
[0.22431934 0.44396499]]]
[[[0.36741016 0.22431934]
[0.22431934 0.44396499]]
[[0.59080731 0.44396499]
[0.44396499 1.05571294]]]]
电子总能： -4.254913579487779
电子总能： -4.20792775552603
电子总能： -4.208584351684131
电子总能： -4.208685329895248
电子总能： -4.208700828901645
电子总能： -4.208703207104221
电子总能： -4.2087035720040795
电子总能： -4.208703627992145
电子总能： -4.208703636582611
系数矩阵：
[[-0.20248149 -1.16783601]
[-0.87660401 0.79775003]]
最终电子总能： -4.208703636582611
最终系统总能： -2.8418364960686695
单电子轨道能量： -1.6328025220748532
可以得知最终的系统总能约为 $-2.8418 \ \mathrm{Ha}$，另外在实空间中，我们对电子密度分布在二维切面上进行了绘制，如图 1 所示。
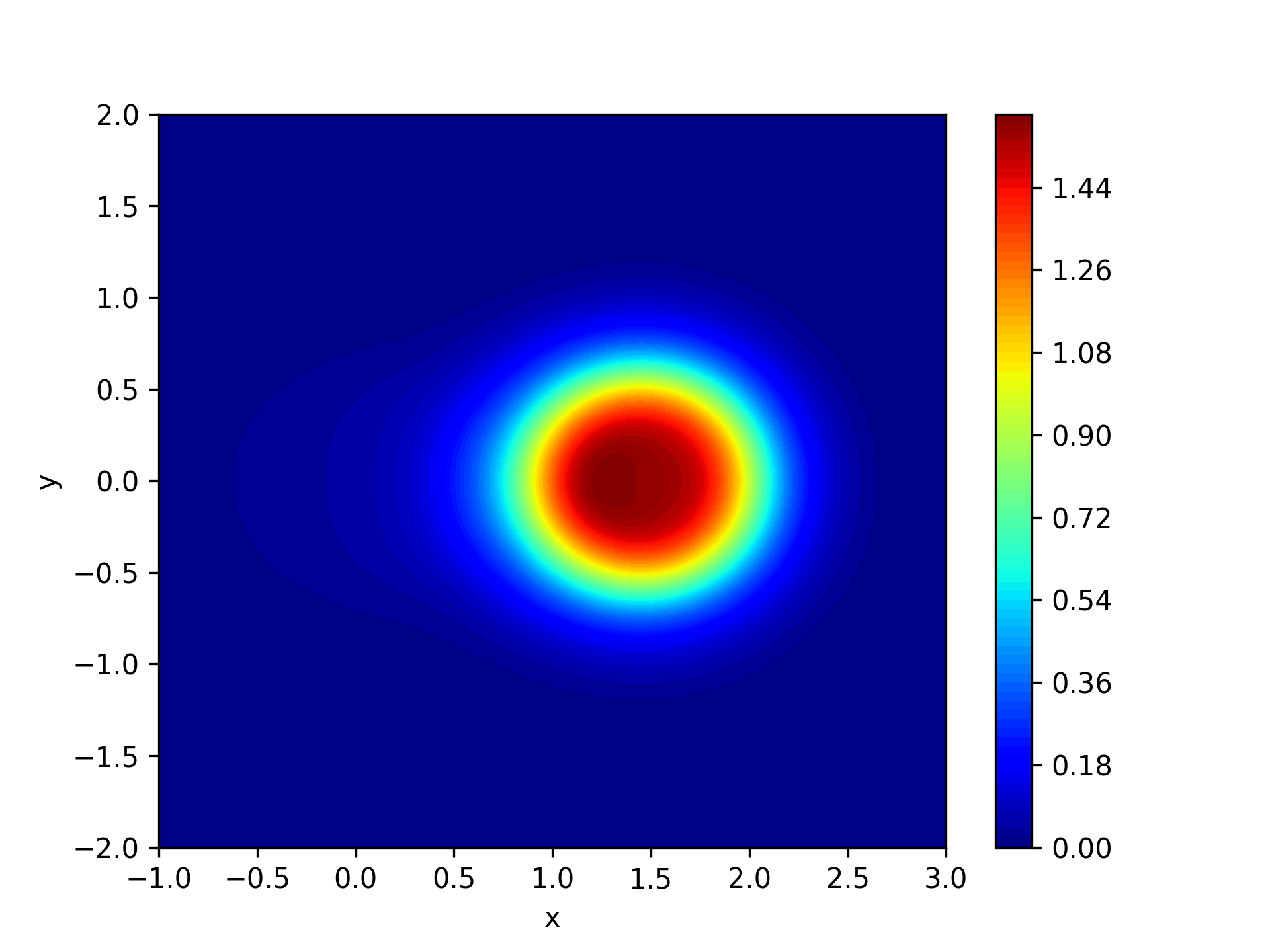图 1 实空间电子密度分布，氢原子位于 $(0, 0, 0)$ 处，氦原子位于 $(1.4632, 0, 0)$ 处，颜色代表电子密度，取二维平面 $z = 0$ 进行绘制
在本题的最后，附上完整的代码如下：
from itertools import product
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import erf
N = 2 # 原子数
M = 3 # Gaussian 函数个数 展开基函数
R = [0, 1.4632] # 原子核坐标
Z = [1, 2] # 原子核电荷数
EXPO = np.zeros((N, M)) # 指数
COEF = np.zeros((N, M)) # 系数
# He 原子
EXPO[1, 0] = 6.362421394
EXPO[1, 1] = 1.158922999
EXPO[1, 2] = 0.3136497915
# zeta = 2.0925 ** 2
# EXPO[1, 0] = 2.22766 * zeta
# EXPO[1, 1] = 0.405771 * zeta
# EXPO[1, 2] = 0.109818 * zeta
# H 原子
EXPO[0, 0] = 3.425250914
EXPO[0, 1] = 0.6239137298
EXPO[0, 2] = 0.1688554040
COEF[0, 0] = 0.1543289673
COEF[0, 1] = 0.5353281423
COEF[0, 2] = 0.4446345422
COEF[1, 0] = COEF[0, 0]
COEF[1, 1] = COEF[0, 1]
COEF[1, 2] = COEF[0, 2]
S = np.zeros((N, N)) # 重叠积分矩阵
T = np.zeros((N, N)) # 动能积分矩阵
Vne = np.zeros((N, N)) # 核-电子相互作用积分矩阵
Vee = np.zeros((N, N, N, N)) # 双电子积分矩阵
for x, y in product(range(N), repeat=2):
for i, j in product(range(M), repeat=2):
expo_sum = EXPO[x, i] + EXPO[y, j]
expo_mul = EXPO[x, i] * EXPO[y, j]
r_norm = np.abs(R[y] - R[x])
rij = (EXPO[x, i] * R[x] + EXPO[y, j] * R[y]) / expo_sum
c = COEF[x, i] * COEF[y, j]
S[x, y] += c * ((4 * expo_mul / expo_sum**2) ** (3/4)) * \
np.exp(-r_norm**2 * expo_mul / expo_sum)
T[x, y] += c * (3 - 2 * r_norm**2 * expo_mul / expo_sum) * 2**(3/2) * expo_mul**(
7/4) * np.exp(-r_norm**2 * expo_mul / expo_sum) / expo_sum**(5/2)
for z in range(N):
rq = np.abs(rij - R[z])
if np.isclose(rq, 0):
Vne[x, y] += -c * 2 * Z[z] / expo_sum / \
np.sqrt(np.pi) * (4 * expo_mul) ** (3/4) * \
np.exp(-r_norm**2 * expo_mul / expo_sum)
else:
Vne[x, y] += -c * Z[z] * (4 * expo_mul / expo_sum**2)**(
3/4) / rq * np.exp(-r_norm**2 * expo_mul / expo_sum) * erf(np.sqrt(expo_sum) * rq)
for i, j, k, l in product(range(N), repeat=4):
for ii, jj, kk, ll in product(range(M), repeat=4):
c = COEF[i, ii] * COEF[j, jj] * COEF[k, kk] * COEF[l, ll]
expo_sum1 = EXPO[i, ii] + EXPO[j, jj]
expo_sum2 = EXPO[k, kk] + EXPO[l, ll]
expo_mul1 = EXPO[i, ii] * EXPO[j, jj]
expo_mul2 = EXPO[k, kk] * EXPO[l, ll]
r_norm1 = np.abs(R[j] - R[i])
r_norm2 = np.abs(R[l] - R[k])
rij = (EXPO[i, ii] * R[i] + EXPO[j, jj] * R[j]) / expo_sum1
rkl = (EXPO[k, kk] * R[k] + EXPO[l, ll] * R[l]) / expo_sum2
rq = np.abs(rij - rkl)
t = 64 * (expo_mul1 * expo_mul2)**(3/4) / (4 * expo_sum1 * expo_sum2)**(
3/2) * np.exp(-expo_mul1 * r_norm1**2 / expo_sum1 - expo_mul2 * r_norm2**2 / expo_sum2)
tt = expo_sum1 * expo_sum2 / (expo_sum1 + expo_sum2)
if np.isclose(rq, 0):
Vee[i, j, k, l] += 2 * c * t * np.sqrt(tt / np.pi)
else:
Vee[i, j, k, l] += c * t / rq * erf(rq * np.sqrt(tt))
print('重叠积分矩阵：\n', S)
print('动能积分矩阵：\n', T)
print('电子与核吸引能矩阵：\n', Vne)
print('双电子积分矩阵：\n', Vee)
H_core = T + Vne # 核势能矩阵
s, U = np.linalg.eig(S)
X = U @ np.diag(1 / np.sqrt(s)) # 变换矩阵
C = np.zeros((N, N)) # 系数矩阵
C[0, 0] = 1
C[1, 1] = 1
energy = 0 # 电子总能
for _ in range(100): # 自洽场迭代
C_old = C
G = np.zeros((N, N))
for i, j, k, l in product(range(N), repeat=4):
G[i, j] += (2 * Vee[i, j, k, l] - Vee[i, l, k, j]) * C[k, 0] * C[l, 0]
F = H_core + G
F_prime = X.T @ F @ X
e, C = np.linalg.eig(F_prime)
# 需要对特征值和特征向量进行升序排序
eigen_id = np.argsort(e)
e = e[eigen_id]
C = C[:, eigen_id]
C = X @ C
energy = 0
for i, j in product(range(N), repeat=2):
energy += C[j, 0] * C[i, 0] * (F[i, j] + H_core[i, j])
# print('系数矩阵：\n', C)
print('电子总能：', energy)
if np.allclose(C, C_old, rtol=1e-8, atol=1e-8):
break
print('系数矩阵：\n', C)
print('最终电子总能：', energy)
print('最终系统总能：', energy + Z[0] * Z[1] / np.abs(R[0] - R[1]))
print('单电子轨道能量：', e[0])
def gaussian(x, alpha, c=1):
'''高斯基函数'''
return c * (2 * alpha / np.pi) ** (3 / 4) * np.exp(-alpha * x ** 2)
def basis_1(x, y, z):
'''H 基函数'''
r = np.abs((x - R[0])**2 + y**2 + z**2)
return sum([gaussian(r, EXPO[0, i], COEF[0, i]) for i in range(M)])
def basis_2(x, y, z):
'''He 基函数'''
r = np.abs((x - R[1])**2 + y**2 + z**2)
return sum([gaussian(r, EXPO[1, i], COEF[1, i]) for i in range(M)])
phi = [basis_1, basis_2] # 基函数列表
# 电子数密度分布图
x = np.linspace(-1, 3, 500)
y = np.linspace(-2, 2, 500)
X, Y = np.meshgrid(x, y)
Z = np.zeros_like(X)
for i, j in product(range(N), repeat=2):
Z += 2 * C[i, 0] * C[j, 0] * phi[i](X, Y, 0) * phi[j](X, Y, 0)
plt.contourf(X, Y, Z, 100, cmap='jet')
plt.colorbar()
plt.xlabel('x')
plt.ylabel('y')
plt.savefig('hartree_fock.png', dpi=300)