Berry 曲率的轨道设计:晶体场诱导的夹点和巨型偶极子
本文是论文的大体内容翻译,会有不少跳过的部分和语句,想要详细研究请看原文
本文缩写较多,故先列于下方表中以供查阅
| 简写 | 英文 | 中文 |
|---|---|---|
| BC | Berry curvature | 贝里 Berry 曲率 |
| BZ | Brillouin zone | 布里渊 Brillouin 区 |
| BCD | Berry curvature dipole | Berry 曲率偶极子 |
| 2DEG | two-dimensional electron gas | 二维电子气 |
| TRIM | time-reversal invariant momenta | 时间反演不变动量 |
| IRREP | irreducible representation | 不可约表示 |
ABSTRACT
Berry 曲率——一个编码固体中电子波函数几何性质的量——是不同的 Hall 霍尔输运现象的核心,包括反常 Hall 效应、非线性 Hall 效应和能斯特 Nernst 效应。在非中心(偏心)晶体排列的非磁性量子材料中,BC 的局域浓度通常与电子和空穴激发的量子叠加的单粒子波函数有关。
在这里,我们证明了在具有轨道自由度的材料中,即使在完全没有空穴激发的情况下,也可以产生局域 BC 浓度。在这些固体中,晶体场以非常低的对称性结构出现,触发了以热点和奇异夹点为特征的 BC,这些特征自然产生了巨大的 BCD 和在时间反演对称条件下的大的非线性输运响应。
INTRODUCTION
非常的省略
在量子现象中,那些与电子波函数的几何性质有关的量子现象无疑起着主要作用。量子几何张量的虚部对应于众所周知的 Berry 曲率,当它在整个 BZ 上积分时,给出了分类二维绝缘体的 Chern number 陈数。在具有部分填充能带的金属系统中,如果系统破坏了时间反演对称性,则所有占据态上的 BC 相加可以导致非零 Berry 相位,这种 Berry 相位控制了磁性金属的反常 Hall 电导的本征部分。在没有外部磁场的情况下,非磁性材料的 BC 电荷输运 diagnostic 诊断需要超越线性响应机制,Hall-like 电流表现为对驱动电场的非线性(二次)响应,其本征贡献由 Berry 曲率偶极子决定,BCD 本质上是动量空间中 Berry 曲率的一阶矩。
一个基本的问题是:即使在完全没有空穴激发的情况下,电子系统是否以及如何在时间反演对称条件下产生强烈的局域 BC 浓度。在这里,我们通过证明具有有效的伪自旋为一的轨道自由度的自旋轨道自由金属系统 spin–orbit free metallic systems with an effective pseudo-spin one orbital degree of freedom 可以出现 BC 热点和特征 BC 奇异夹点,从而给出了这个问题的肯定答案,它们产生的偶极子的数量级比 2DEG 中的自旋轨道耦合所产生的偶极子的数量级大。
RESULTS
Model Hamiltonian from symmetry principles
首先考虑一个一般的只有自旋自由度的二维单谷两能级系统,相应的能谱被假定为精确地表示所讨论的金属的费米能级附近的电子能带。在时间反演不变动量 time-reversal invariant momenta (TRIM) 附近的有效 Hamiltonian 可以使用跟踪晶体点群对称性的传统 \(\vb*{k} \vdot \vb*{p}\) 微扰理论来得到,具体而言,假设低能导带以布里渊区 Brillouin zone (BZ) 的 $\Gamma$ 点为中心,处理的是具有 $\mathrm{C}_{3v}$ 点群(生成元包括三重旋转和一个垂直镜面对称)对称性的偏心晶体。
考虑到时间反演对称性 \(\mathcal{T} = \ii \sigma_y \mathcal{K}\)($\mathcal{K}$ 是复共轭)和 $\mathrm{C}_{3v}$ 点群对称性,Hamiltonian 展开到 \(\vb*{k}\) 的一阶项有形式 \(\mathcal{H}(\vb*{k}) = a_R (k_x \sigma_y - k_y \sigma_x)\),但其 Dirac 锥能谱违反了费米子加倍定理 fermion doubling theorem(一个局域自由费米子晶格系统,若其作用量具有手征性以及平移对称性则费米子数会加倍),因此它只能出现在三维强拓扑绝缘体的孤立面 isolated surface 上,确实,它与 $\mathrm{Bi}_2 \mathrm{Se}_3$ 材料类中拓扑绝缘体的表面态的有效哈密顿量一致。
在一个真正的二维系统中,Hamiltonian 应当有一个动量平方的附加项,使每个能量的状态数增加一倍,而时间反演对称性意味着动量平方项应该与单位矩阵耦合,则我们得到了众所周知的具有类 Rashba 自旋轨道耦合的二维电子气的 Hamiltonian: \(\begin{equation} \mathcal{H} (\vb*{k}) = \frac{\hbar^2 k^2}{2m} \sigma_0 + a_R (k_x \sigma_y - k_y \sigma_x) . \end{equation}\) 其相应的能谱是由两条错位的抛物线构成的,这展示在了图 1a 中。这个 Hamiltonian 只满足了晶体对称性要求,不能预测任何有限的 Berry 曲率 Berry curvature (BC) 的局部浓度,因为矢量 \(\vb*{d} = (-a_R k_y, a_R k_x, 0)\) 被限制在二维平面上。有两种方式去“抬起” \(\vb*{d}\) 矢量到平面外,从而引发非零 BC,第一种方法是添加恒定质量 $\Delta \sigma_z$,可以通过施加平面外磁场或者诱导长程磁序来实现,此时 BC 会在 TRIM 处出现热点 hot-spot 和圆形分布,见图 1b、图 1c;第二种方式是考虑动量立方项和 $\sigma_z$ 耦合的贡献,这产生了角度依赖的 BC 分布,但这种由于晶体各向异性触发的 BC 没有热点。这样看来,在具有常规准粒子和单个内部自由度的系统中,似乎打破时间反演对称性是出现大的局域 BC 的必要条件?
本文提出,在有轨道自由度的系统中,即使在时间反演对称性存在下,也完全允许形成 BC 热点。作为例子,考虑一个 $\mathrm{p}$ 轨道系统,在一般的中心对称晶体中,远离 TRIM 的轨道杂化只能出现在动量平方项上,但注意到在偏心晶体中,动量线性的轨道间混合项是对称性允许的,这些混合项通常被称为轨道 Rashba 耦合,这将带给我们时间反演对称性下的 BC 热点。
和刚刚一样,假设一个拥有 \(\mathrm{C}_{3v}\) 点群对称性的偏心晶体,由于 \(\mathrm{SU}(2)\) 自旋对称性守恒,电子实际上是无自旋的,也就是说,我们消除了自旋轨道耦合。远离 TRIM 的有效 Hamiltonian 可以使用对称性约束来得到,具体而言,任何 \(3 \times 3\) 的 Hamiltonian 都可以用九个 Gell–Mann 矩阵 \(\Lambda_i\) 来展开:\(\mathcal{H} (\vb*{k}) = \sum_{i=0}^{8} b_i(\vb*{k}) \Lambda_i .\) 故考虑到动量线性的有效 Hamiltonian 表示为 \(\begin{equation} \mathcal{H} (\vb*{k}) = \Delta \qty(\Lambda_3 + \frac{1}{\sqrt{3}} \Lambda_8) - a_R \qty(k_x \Lambda_5 + k_y \Lambda_2) . \end{equation}\) 式中,参数 $\Delta$ 量化了 \(\mathrm{p}_{x,y}\) 双重态和 \(\mathrm{p}_z\) 单态之间的能级分裂。我们对空穴和电子不共存的系统感兴趣,故接着引入对三个能带有相同有效质量的一项 \(\hbar^2 k^2 \Lambda_0 / (2m)\),随后的 Hamiltonian 可以看作是 Rashba 2DEG 到 \(\mathrm{SU}(3)\) 系统的推广。对应的能谱见图 1d,这与时间反演对称性破缺的二维电子气的结果相似,但计算表明,对应的 BC 对所有动量都是零。下面的关键是,只依赖于通过将晶格点群降低到 \(\mathrm{C}_s\) 产生的晶体场效应,我们发现有效 Hamiltonian 为 \(\begin{equation} \begin{aligned} \mathcal{H} (\vb*{k}) =& \frac{\hbar^2 k^2}{2m} \Lambda_0 + \Delta \qty(\Lambda_3 + \frac{1}{\sqrt{3}} \Lambda_8) + \Delta_m \qty(\frac{1}{2}\Lambda_3 - \frac{\sqrt{3}}{2} \Lambda_8) \\ &- a_R \qty(k_x \Lambda_5 + k_y \Lambda_2) - a_m k_x \Lambda_7 . \end{aligned} \label{math:1} \end{equation}\) 不失一般性,在接下来的讨论中,我们只考虑单参数 $a_R$。在上面的 Hamiltonian 中,我们忽略了常数项 $\propto \Lambda_1$,对于具有高温三角结构的材料,其振幅 $\Delta_1$ 预计与 $\Delta_m$ 的量级相同,在这种情况下,其对于能谱和 BC 性质的贡献很小(见补充材料 note 1),可以忽略。图 1e 是能谱,其表明晶体对称性的降低的影响是双重的:第一,在 \(\mathrm{p}_{x, y}\) 间有一个附加的能级分裂,这意味着在 BZ 的 $\Gamma$ 点上所有能级都是单一简并的 singly degenerate;第二,两个 \(\mathrm{p}_{x, y}\) 轨道沿着 BZ 的镜像对称 $k_x = 0$ 线有能带简并,这会导致 BC 奇异夹点 singular pinch point 的产生,见图 1f 和补充材料 note 2。注意到 BC 有热点,其源与汇在任何镜像对称费米面上平均为零,这是时间反演对称性所要求的。
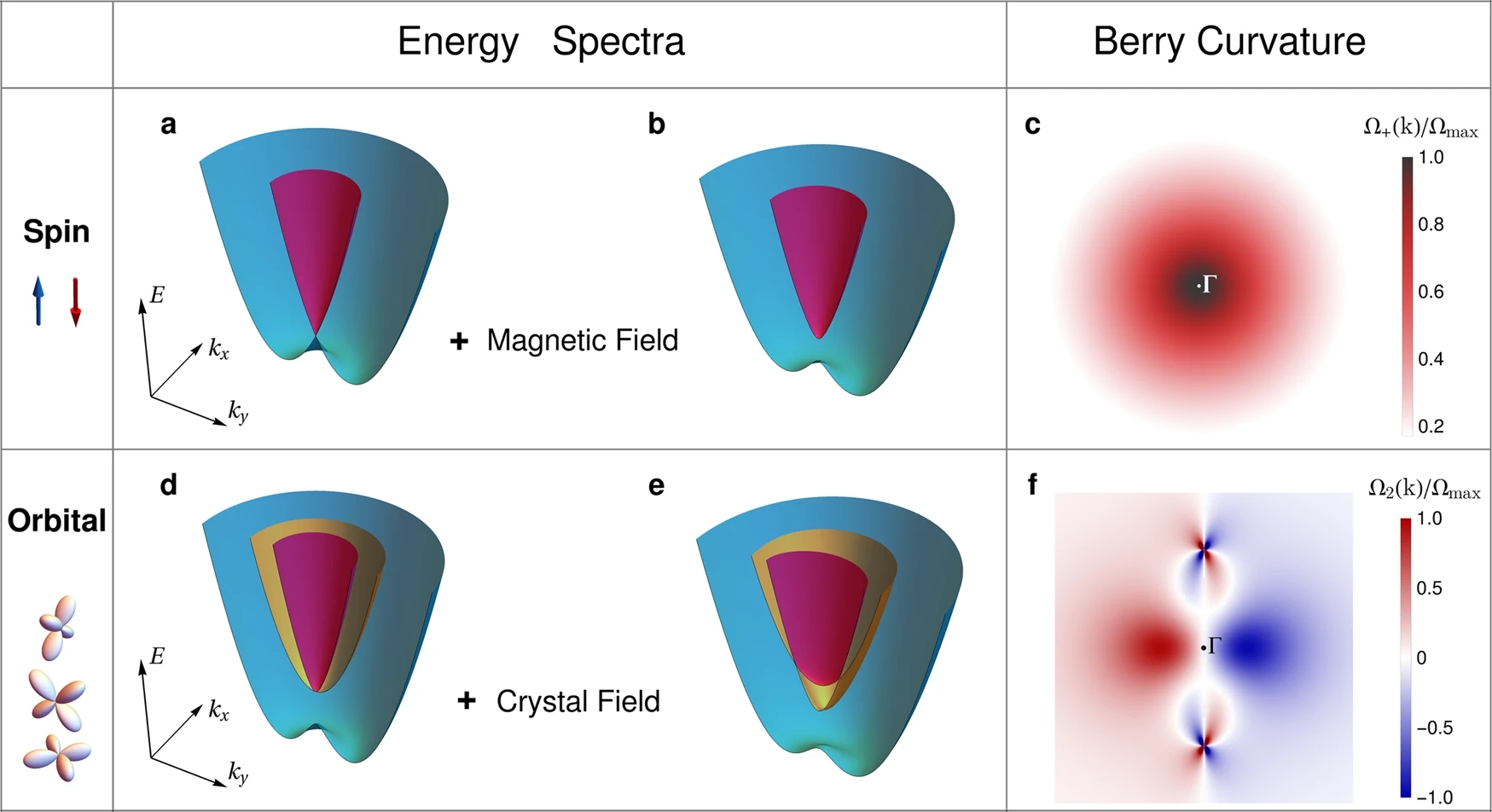 图 1 Berry 曲率的自旋和轨道机制
图 1 Berry 曲率的自旋和轨道机制
Material realizations
此部分基本省略(所以也没有图 2 了),是符合条件的材料的一些介绍
好像漏了很重要一段,算了,直接口述吧:选择 $(111) \ \text{LAO/STO}$ 异质界面,氧化物中的低温相变降低了晶体的对称性,\(\text{STO}\) 在 $105 \ \text{K}$ 有从立方相到四方结构的相变,打破了三重旋转对称性,保留了一个镜像对称性,这就实现了之前所说的对称性降低的要求
在分析 BC 起源和物理结果以及特征夹点之前,我们现在介绍一种自然有轨道自由度和所需的低晶格对称性的材料——过渡金属氧化物 transition metal oxides 的 $[1 1 1]$ 界面,其具有 $t_{2g}$ 轨道特征的二维 $\mathrm{d}$ 电子系统,例如 $\mathrm{SrTiO}_3$、$\mathrm{K Ta O}_3$ 和 $\mathrm{SrVO}_3$ 基底的异质结。
在这些材料的高温立方相中,八面体晶体场将低能物理钉扎到简并 $t_{2g}$ 流形上,生成一个有效角动量一个子空间,与上面讨论的 $\mathrm{p}$ 轨道完全相同。界面对称性的降低提升了 $t_{2g}$ 的能量简并,改变了它们的轨道性质。在 $[1 1 1]$ 界面,过渡金属原子形成具有三个交错层的堆积三角形晶格,这导致了一个三角形的平面晶场,杂化了 $\ket{xy}, \ket{xz}, \ket{yz}$ 轨道,形成一个一维 IRREP 和一个二维 IRREP。
Berry curvature dipole
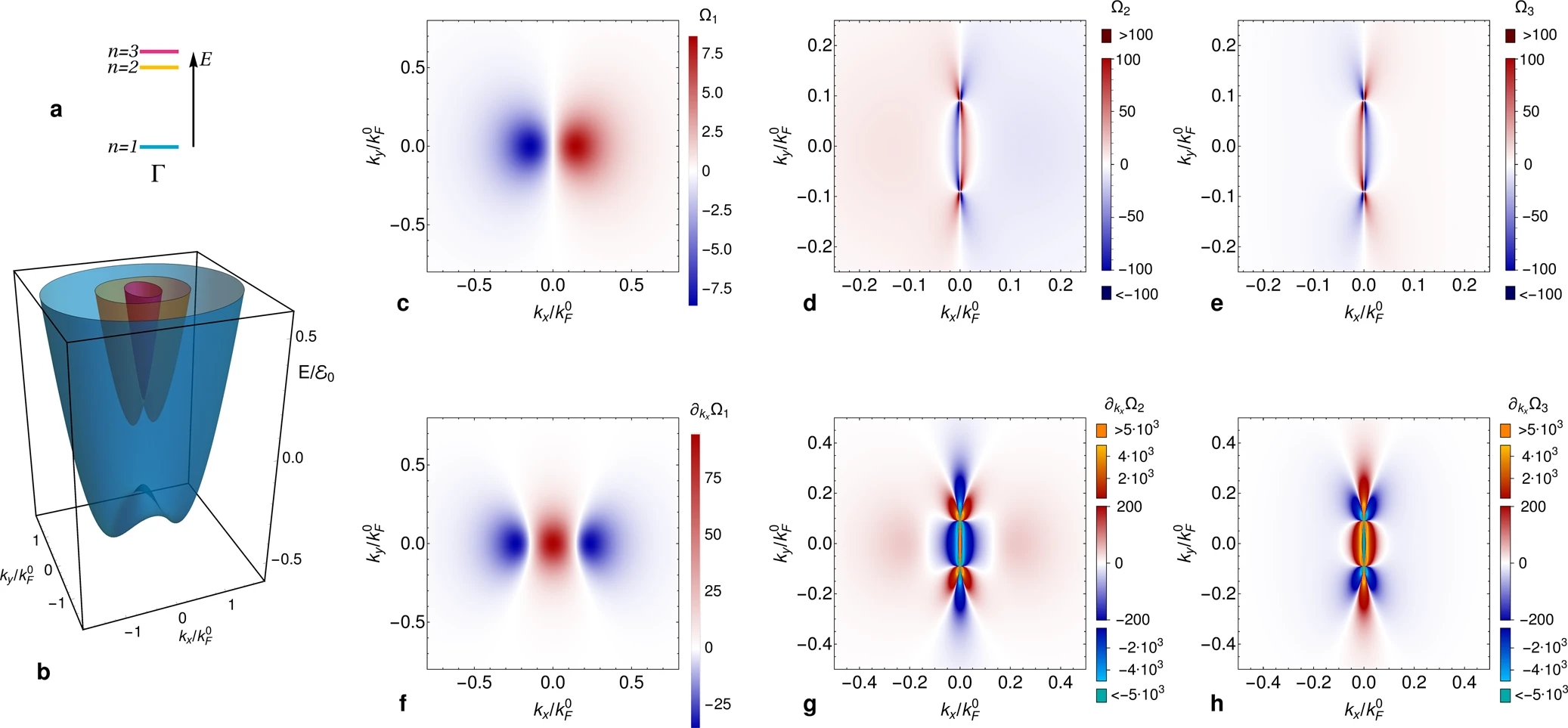 图 3 Berry 曲率热点和夹点的轨道设计
图 3 Berry 曲率热点和夹点的轨道设计
在确定了 $(111)$ 取向的氧化物异质界面是理想的材料平台后,接下来我们分析了 BC 的特性和它的一阶矩。我们首先注意到,在二能级自旋系统的情况下,自旋分裂能带的局部 Berry 曲率,如果非零,则是相反的。由于两个自旋能带在每个费米能区的同时存在,除了被一个自旋带占据的动量外,自旋分裂能带抵消了各自的局域 BC。在近在咫尺的 $\mathrm{SU}(3)$ 系统中,有一个类似的求和规则,即在每一个动量 \(\vb*{k}\) 处,三个能带的 BC 求和为零。然而,如上所述,轨道能带不受费米子乘法定理的约束,在某些能量范围内,占据单个轨道能带时,BC 不会抵消(参考图 3a, b)。
自旋和轨道导致的 BC 二者之间还有一个关键差别,与生成一个角动量为一的子空间的 $\mathrm{SU}(3)$ 系统不同,在 $\mathrm{SU}(2)$ 自旋系统中,对称结构常数为零。因此,只要不考虑晶体各向异性,星积 star product \(\vb*{b_k} \star \vb*{b_k}\) 的消失就阻止了具有时间反向对称性的 BC 的出现。而另一边,对于 $\mathrm{SU}(3)$,所有三个纯虚数的 Gell-Mann 矩阵 $\Lambda_{2,5,7}$ 的存在,再加上“质量”项 $\Lambda_{3, 8}$,在甚至只考虑动量线性项的情况下,是出现时间反演对称性 BC 中心 concentrations 的充分条件。然而,这严格要求必须打破所有的旋转对称性。
接下来,我们从最低能带开始分析了局域 BC 的性质,该能带对应于 $(111) \ \text{LAO/STO}$ 异质界面的 $(\ket{xy} + \ket{xz} + \ket{yz}) / \sqrt{3}$ 态($\text{LAO}$ 就是 $\text{LaAlO}_3$ 铝酸镧,$\text{STO}$ 就是 $\text{SrTiO}_3$ 钛酸锶)。图 3c 是特征 BC 剖面,它显示了中心在 $k_y = 0$ 线上的两个相反极点,由于 BC 作为任何真正的伪标量在垂直镜像对称运算下必须是奇的 odd,即 $\Omega(k_x, k_y) = - \Omega(-k_x, k_y)$,所以源和汇到镜像对称线 $k_x = 0$ 的距离是相等的。注意到,时间反演对称性和垂直镜像的组合意味着 BC 将甚至有变换 $k_y \rightarrow − k_y$,从而保证 BC 热点将以 $k_y = 0$ 线为中心。源和汇的有限 $k_x$ 值与能带 $n=1$ 和 $n=2$ 之间的(直接)能隙最小的点是吻合的(见图 3a, b 和补充材料 note 2),因此轨道间混合 interorbital mixing 是最大的。
BC 的性质显然反映在 BCD 局域浓度 $\pp_{k_x} \Omega(k_x, k_y)$ 中:它在 BZ 的中心有一个非常强的局域的正区,并被有限 $k_x$ 处的两个镜像对称的负区所中和,见图 3f。接下来,让我们考虑由三重旋转对称破缺而分裂的两个简并 $e’_g $ 态产生的 BC 分布。图 3d 是两个能带中低能带的 BC 剖面:它完全由 $k_x=0$ 线上的镜像对称保护简并引起的 BC 夹点所控制。BC 在夹点周围还显示出节环 nodal ring,因此在奇点周围具有特征性的 \(\mathrm{d}\) 波特征。这可以通过围绕两个与时间反演相关的简并来构建 \(\vb*{k} \vdot \vb*{p}\) 理论来理解,为此,我们首先回顾从 \(e'_{g}\) 态得到的两个能带有相反的沿着 BZ 的全镜面线 \(k_x \equiv 0\) 的 \(\mathcal{M}_x\) 镜像本征值,因此,在接近简并的情况下,$\mathcal{M}_x$ 可以被表示为 $\sigma_z$,其中 $\mathcal{M}_x$ 变换导致 $k_x \rightarrow - k_x$ 且 $k_y$ 不变。在接近简并的情况下,一个有效的二能带模型必须有如下形式的领头项: \(\begin{equation} \mathcal{H}_{\text{eff}} = v_x k_x \sigma_x + \beta k_x \delta k_y \sigma_y + v_y \delta k_y \sigma_z , \end{equation}\) 式中,$\delta k_y$ 是相对于镜像保护的简并测量的动量,另外,我们忽略了与 $k^2 \sigma_0$ 耦合的二次项,因为它不影响 BC。使用二能带模型的通常的 BC 公式,可以证明上面的 Hamiltonian 是由带有两条节线 nodal line 的零动量夹点和 \(\mathrm{d}\) 波特征来表征的。有趣的是,这也意味着在夹点附近反转 \(\vb*{k}\) 符号的有效时间反演对称性被打破。也许更重要的是,\(\mathrm{d}\) 波特征意味着紧邻夹点附近有非常大的 BCD 密度,见图 3g。当考虑最高能带时,也会遇到类似的性质,不同之处在于,夹点具有相反的角度相关性(见图 3e),因此 BCD 密度具有相反的符号(见图 3h)。
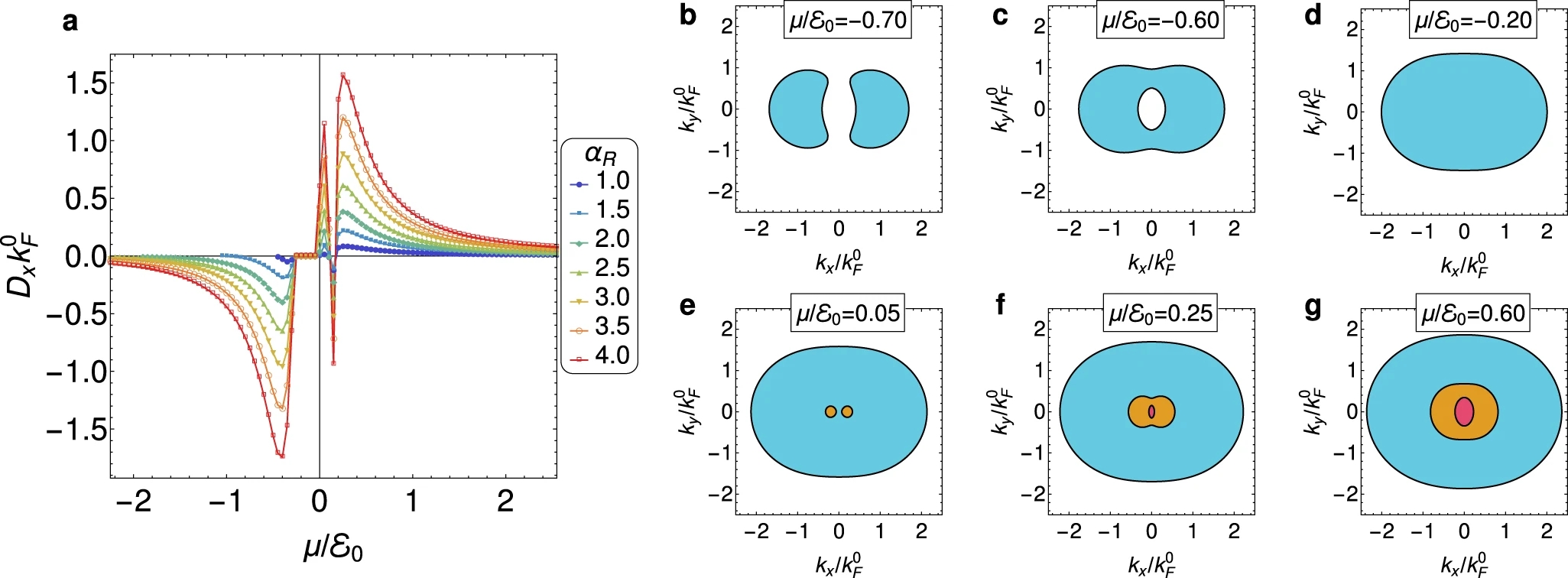 图 4 Berry 曲率偶极子和费米线的拓扑结构
图 4 Berry 曲率偶极子和费米线的拓扑结构
有了不同能带的 BC 和 BCD 密度分布,我们最后讨论了在 BCD 中的特征指纹 characteristic fingerprint,定义为 \(D_x = \int_{\vb*{k}} \pp_{k_x} \Omega(\vb*{k}) f_0\),其中 \(\int_{\vb*{k}} = \int \dd[2]{k} / (2 \pi)^2\),以及 $f_0$ 是平衡 Fermi-Dirac 分布函数。通过连续扫描费米能量,我们发现 BCD 显示出尖点和拐点(见图 4a),这是 Lifshitz 跃迁(Lifshitz 相变是费米面在能带结构或费米能变化的驱动下发生的电子拓扑跃迁)及其相关的 van Hove 范霍夫奇点的直接结果(见补充材料 note 3)。从第一能带的底部开始,BCD 的幅度连续增加,直到它达到最大值,此时偶极子大于 2DEG 的费米动量的倒数 $1/ k_{F}^0$,从而获得相对于 Rashba 2DEG 的三个数量级的增强。
Fermi pockets 费米口袋(或 Fermi surface 费米面)是费米能量在 Brillouin 区的轮廓。根据准粒子的有效质量 \(m^{*}\),费米口袋可分为 electron pocket 电子口袋(如果 \(m^{*} > 0\))和 hole pocket 空穴口袋(如果 \(m^{*} < 0\))。
在这个区域中,有两个不同的费米线围绕着有限 \(\vb*{k}\) 值的电子口袋 electronic pocket(参考图 4b),随后在动量空间中的两个不连通的区域上合并(参考图 4c)。由于 BZ 中心附近的态没有被占据,BCD 完全被图 3f 的两个镜像对称的负热点所支配。通过进一步增加化学势,内部费米线在 $\Gamma$ 点处塌陷,因此发生第一次 Lifshitz 跃迁(参考图 4d)。在这种情况下,由于 BZ 中心周围的强大的正 BCD 密度区域抵消了镜像对称的负热点,因此 BCD 具有指数级的小值。再加化学势,第二个 Lifshitz 跃迁发生了,表明第一个 $e_g$ 能带被占据,其中两个口袋以 $k_y = 0$ 线为中心。这个 Lifshitz 相变与 BCD 的快速增加相吻合,这是由于来自图 3g 的 BC 节环外部的局部 BCD 密度区域的贡献。随后的尖锐负峰来自第三次 Lifshitz 跃迁,过程中,第二个能带的两个电子口袋合并,并几乎同时出现了以 $\Gamma$ 为中心的第三个能带的一个微小口袋(见图 4f)。通过计算能带分辨的 BCD(见补充材料 note 4),我们发现正是这个小口袋导致了负尖峰。对于足够大的化学势,BCD 产生一个额外的峰,对应于图 4g 的费米面学 fermiology。由于 BC 局部求和规则,靠近 BZ 中心的动量对 BCD 没有贡献,故产生了这个同样大于 $1/ k_{F}^0$ 的峰值。另一方面,BC 节环外部的区域没有被第三个能带占据,因此具有净的正 BCD 局域密度。注意到,BCD 通过增加轨道间混合参数 $a_R$、$a_m$ 而被放大,但保持类似的性质(见图 4 和补充材料 note 3)。
最后,让我们讨论一下自旋轨道耦合的作用,它可以被包括在我们的 Hamiltonian 式 $\eqref{math:1}$ 中作为 \(\mathcal{H}_{\text{so}} = \lambda_{\text{so}} (L_x \otimes \tau_x + L_y \otimes \tau_y + L_z \otimes \tau_z)\),其中 $\lambda_{\text{so}}$ 是自旋轨道耦合强度,$L=1$ 的角动量矩阵对应于 Gell-Mann 矩阵 $\Lambda_2, \Lambda_5, \Lambda_7$,以及 Pauli 矩阵 $\tau_{x,y,z}$ 作用于自旋空间。它的影响可以用传统的简并微扰理论来分析,在 BZ 的中心 \(\mathcal{H}_{\text{so}}\) 是完全不活跃的——Hamiltonian 式 $\eqref{math:1}$ 的本征态是轨道本征态,且轨道空间中非对角项 $\Lambda_2, \Lambda_5, \Lambda_7$ 在 \(\lambda_{\text{so}}\) 中不能给出任何的一阶修正。当动量有限时,情况就不同了,这两个自旋轨道自由简并本征态是不同轨道的叠加(由于轨道 Rashba 耦合),因此,自旋轨道耦合项将解除它们的简并,导致能带的类 Rashba 分裂。
为了探索这种自旋分裂对 BC 的影响,让我们用 \(\ket{\psi_0^{\uparrow}(\vb*{k})}\) 和 \(\ket{\psi_0^{\downarrow}(\vb*{k})}\) 表示两个自旋轨道自由度简并的本征态,注意 $\ket{\psi_0}$ 是轨道自由度的三分量旋量。当微扰地考虑自旋轨道耦合时,本征态将是自旋简并本征态的叠加,并且通常有 \(\begin{equation} \begin{aligned} \ket{\psi^{+}(\vb*{k})} & = \cos{\theta(\vb*{k})} \ee^{\ii \phi(\vb*{k})} \ket{\psi_0^{\uparrow}(\vb*{k})} + \sin{\theta(\vb*{k})} \ket{\psi_0^{\downarrow}(\vb*{k})} , \\ \ket{\psi^{-}(\vb*{k})} & = - \sin{\theta(\vb*{k})} \ee^{\ii \phi(\vb*{k})} \ket{\psi_0^{\uparrow}(\vb*{k})} + \cos{\theta(\vb*{k})} \ket{\psi_0^{\downarrow}(\vb*{k})} . \end{aligned} \end{equation}\) 这里的相位 $\phi$ 和角度 $\theta$ 的动量依赖是轨道 Rashba 耦合的副产物:自旋轨道耦合的效应在轨道空间中是非对角的,受本征态的动量依赖的轨道内容的调制。两个自旋分裂态的 abelian 阿贝尔 Berry connection 联络 \(\mathcal{A}^{+, -}_{k_x, k_y} = \braket{\psi^{+, -}(\vb*{k})}{\ii \pp_{k_x, k_y} \psi^{+, -}(\vb*{k})}\) 因此包含两项:第一项是与自旋无关的 Berry 联络 \(\mathcal{A}^{0}_{k_x, k_y} = \braket{\psi(\vb*{k})}{\ii \pp_{k_x, k_y} \psi(\vb*{k})}\);第二项则与相位 $\phi$ 和角度 $\theta$ 有关。这种 Berry 联络对于 $+, -$ 态是相反的,与二能级自旋系统的 Berry 联络是一致的。这也意味着能带的一个 Kramers 对(Kramers’ pair 就是时间反演对称性导致简并的两个态)的 Berry 曲率 \(\Omega^{+, -} (\vb*{k}) = \Omega(\vb*{k}) \pm \Omega_{\text{so}} (\vb*{k})\)。Berry 曲率 \(\Omega_{\text{so}} (\vb*{k})\) 对于时间反演对的贡献是相反的,净效应仅来自两个配对能带的费米线之差。然而,纯轨道 BC \(\Omega(\vb*{k})\) 可以直接从式 $\eqref{math:1}$ 中计算,它求和而加倍了。因此,在存在微弱但有限的自旋轨道耦合的情况下,图 4 中的 BCD 值简单地翻了一番。
DISCUSSION
在这项研究中,我们已经展示了一个内在的途径,在时间反演对称的情况下,仅利用电子与原子核结合时获得的轨道角动量,来设计了大浓度的 Berry 曲率。事实上,我们已经证明了由轨道自由度触发的 Berry 曲率既有热点也有奇异夹点。此外,由于晶体对称性的限制,Berry 曲率自然配备了一个不为零的 Berry 曲率偶极子。这些特性使量子非线性 Hall 效应提高了三个数量级。
我们的研究结果对被称为轨道电子学的凝聚态物理学的发展领域产生了巨大的影响。固体中的电子可以通过利用其固有自旋或轨道角动量来携带信息。使用电子自旋产生、检测和处理信息是自旋电子学的基础。我们在研究中揭示的 Berry 曲率分布预计也会触发轨道 Hall 效应,该效应源于电子波函数的几何性质,可以通过轨道自由度来操纵。这为轨道电子设备打开了许多可能性。考虑到我们的发现可以应用于一大类材料,其电子性质可以用有效的 $L=1$ 轨道多重态来描述,这一点甚至更有意义。这包括其它复杂的氧化物异质界面以及可以利用 $\mathrm{p}$ 轨道的自旋轨道自由半导体。
METHODS
Representation of the Gell–Mann matrices in the symmetry groups
除了单位矩阵 $\Lambda_0$,其它八个 Gell-Mann 矩阵定义为: \(\begin{equation} \begin{aligned} \Lambda_1 = \mqty[0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0] , \quad \Lambda_2 = \mqty[0 & -\ii & 0 \\ \ii & 0 & 0 \\ 0 & 0 & 0] , \\ \Lambda_3 = \mqty[1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0] , \quad \Lambda_4 = \mqty[0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0] , \\ \Lambda_5 = \mqty[0 & 0 & -\ii \\ 0 & 0 & 0 \\ \ii & 0 & 0] , \quad \Lambda_6 = \mqty[0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0] , \\ \Lambda_7 = \mqty[0 & 0 & 0 \\ 0 & 0 & -\ii \\ 0 & \ii & 0] , \quad \Lambda_8 = \mqty[\frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 \\ 0 & 0 & \frac{-2}{\sqrt{3}}] . \\ \end{aligned} \end{equation}\) 由于我们考虑的是由于 $\mathrm{SU}(2)$ 自旋对称性而实际上没有自旋的电子,时间反演算符可以表示为 $\mathcal{K}$。因此,三个矩阵 $\Lambda_{2,5,7}$ 在时间反演对称下是奇的,其余都是偶的;类似有 $\Lambda_{1,2,3,8}$ 在垂直镜面对称下是偶的,$\Lambda_{4,5,6,7}$ 是奇的。考虑三重旋转对称性,转动算符 $\mathcal{C}_3 = \exp[2 \pi \ii \Lambda_7 / 3]$,根据对易关系可以发现 ${\Lambda_1, \Lambda_4}$、${\Lambda_2, \Lambda_5}$ 和 ${\Lambda_6, \frac{1}{2} \Lambda_3 - \frac{\sqrt{3}}{2} \Lambda_8 }$ 在三重旋转对称下表现得像矢量,因此形成了二维 IRREPS。
还有两块内容,以及补充材料,略
-
Mercaldo, M. T., Noce, C., Caviglia, A. D., Cuoco, M. & Ortix, C. Orbital design of Berry curvature: pinch points and giant dipoles induced by crystal fields. npj Quantum Mater. 8, 1–9 (2023). ↩